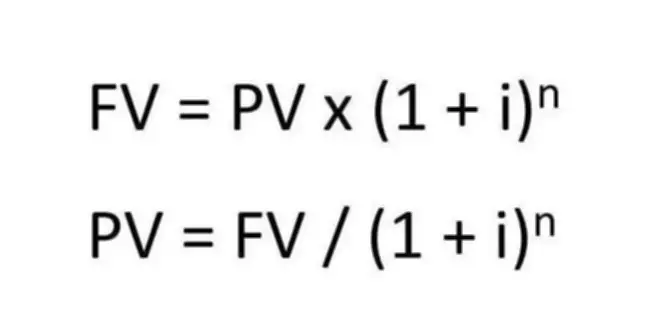Present Value of a Single Amount: Calculation and Formula

In financial decision-making, whether personal or for business, it is crucial to take timing into account. If you could invest $1,000 today and receive $1,500 in 2 years, would that be a worthwhile deal? If you are offered a 10% discount to switch from monthly payments to an annual prepayment, should you take it? “Present value” is a concept that can help you answer questions like these with precision and confidence. Present value tells you how much an amount of money is worth after taking timing into account. The basic idea is simple: the same amount of money can be worth more or less depending on when it is received.

Investors compare the present value of potential deals to decide which ones are worthwhile. Executives use present value when deciding if an expensive project is worth the cost. Borrowers use it to decide whether it makes sense to take a loan at a certain interest rate. Present value is one of the most important concepts in the financial world and is always used when evaluating financial risks and opportunities.

Present Value Definition

The present value of a single amount is defined as the current worth of a single payment or series of payments to be received at a later date, given a specific adjustment for timing based on assumptions about interest rates and inflation. For example, if someone offered you 1 million dollars today versus 1 million dollars 20 years from now, you would need to be able to compare the worth of $1 million today versus the worth of $1 million in 20 years. Time can make all the difference when assessing which decisions are worthwhile.  In order to make the best financial decisions, a business should be able to accurately calculate the worth of a future sum of money in terms of what its current worth would be.

Present Value of Money Formula

When considering the present value of a single amount, we want to determine what this amount will be worth in the future. The time value of money tells us that the future value of money is usually worth less than the current value. How much less? A simple formula helps us calculate the difference.

The future value of a single amount is equal to the amount of money invested or saved, multiplied by one plus the interest rate to the nth power, where n is the number of compounding periods during which the principal is held or invested. If there is more than one compounding per year, you would divide the interest rate by the number of compoundings per year to get the i value and multiply the number of years by the number of compoundings per year to get the n value.

The future value formula can also be modified to figure out the present value. The present value of future cash flow is equal to that future cash flow divided by one plus the interest rate to the nth power. This second formula calculates the current value of an amount you will have in the future, given a specific interest rate.There is a relationship between all the factors involved in the calculation. For a given interest rate, the longer the time period, the lower the present value. For a given time period, the higher the interest, the lower the present value.

Business owners should consider these calculations when making financial decisions, as well as several other variables: the amount of time at their disposal, the risk factor of the business environment, and what interest and inflation rates to expect during the period that the money is held or invested.

How to Calculate Present Value?

Let’s return to our original example, in which we must choose between receiving $1 million today or 20 years from now.  We can now use the formula explained above to calculate the present value. Since we do not know an interest rate value, we will assume it is 10%. (10% is expressed as a decimal amount, 0.1, in the formula below.)

PV = 1,000,000 / (1 + 0.1)20

PV = $148,643.63

The original $1 million depreciates due to the time value of money. As you can see, if the 10% discount was relevant, your 1 million dollars will be worth significantly less in 20 years. It is a stark choice. This example alone should hopefully demonstrate the power of time on the value of a single amount, and why it is therefore such an important variable for business owners and bookkeepers to consider.

Consider another example, in which we use the same formula for a slightly different purpose. Jake wants to have $1,500 in ten years in order to buy a camera. He wants to invest in an account that earns 8% interest compounded annually. Given the rate and period of time, how much money should Jake invest today in order to achieve this goal? We input the given data into the formula to calculate the answer.

PV = 1,500 / (1 + 0.08)10

PV = $694.79

According to our calculation, Jake would need to invest $694.79 today to have $1,500 in ten years. However, there is another, easier way to calculate the present value.  You can refer to a particular table to find the present value factor. For this calculation, you would simply multiply the future value by the factor to get the present value. The result, as you can see below, is exactly the same.

PV = 1,500 x 0.4632

PV = $694.8

Whether you’re preparing financial forecasts to impress potential investors, or deciding whether to take a loan or make a big purchase, understanding present value is crucial. Fortunately, you don’t have to do these financial calculations yourself. An experienced accountant can help. Contact BooksTime to learn how we can take care of the number-crunching for you. That way, you’ll save time and get back to what you care about most.